时间常数分析法
时间常数τ:电路中每一个结点所对应的电容及与之并联的电阻的乘积
开路时间常数法:适用于-3dB高频带宽,计算每一个开路时间常数$\tau_{oi}=R_{oi}C_i$
- 画出等效电路
- 逐个求解从各电容两端看的等效电阻
- 求解时将电路中其它起高频带宽限制作用的电容进行开路处理,并将独立信号源设为无效
- 求解每个电容的开路时间常数及对应的上限截止频率$f_{Hi}$
- 写出高频段电压放大倍数的传递函数$A_u(s)=A_{uM}\prod\frac{1}{1+jf/f_{Hi}}$
短路时间常数分析法适用于-3dB低频带宽,计算每一个开路时间常数$\tau_{oi}=R_{oi}C_i$
- 画出等效电路
- 逐个求解从各电容两端看的等效电阻
- 求解时将电路中其它起高频带宽限制作用的电容进行短路处理,并将独立信号源设为无效
- 求解每个电容的开路时间常数及对应的下限截止频率$f_{Hi}$
- 写出低频段电压放大倍数的传递函数$A_u(s)=A_{uM}\prod\frac{1}{1+jf/f_{Li}}$
放大电路总的传递函数:$A_u(s)=A_{uM}\cdot\prod\frac{1}{1+jf/f_{Hi}}\cdot\prod\frac{1}{1+jf/f_{Li}}$
4-9 放大电路的频率特性
典型频率特性曲线
- $\dot{A_{usM}}$中频放大倍数
- $f_L$:下限截止频率
- $f_H$:上限截止频率
- Δf:通频带(BW)
常用波特图分析。特点:
- 折线化
- 对数分度
- 乘法变加法
频率失真
分类:
- 幅频失真
- 相频失真
- 组合失真
产生原因:
- 电抗性元件
- β
三极管的高频参数
混合π型高频小信号模型
等效模型

参数计算
- $g_m=\frac{\beta}{r_{b’e}}$
单向化

电流放大系数β的频率响应
- 共射截止频率$f_\beta=\frac{1}{2\pi{r_{b’e}}(C_{b’e}+C_{b’c})}$
- 特征频率$f_T\approx\beta_0f_\beta$
理想运放的技术指标
开环差模增益:$A_{od}=\infty$
差模输入电阻:$r_{id}=\infty$
输出电阻:$r_o=0$
共模抑制比:$K_{CMR}=\infty$
一般在原理性分析时,运算放大器都可视作理想的。
在线性区工作时:
- 虚短:==$u_o=A_{od}(u_+-u_-)$==,线性工作区域下可以把输入端看作等电位
- 虚断:输入电阻趋近无穷,$i_+=i_-=0$,线性状态下可把两输入端看作开路。
在非线性区工作时:
- $u_+>u_-时,u_o=+U_{OPP}$
- $u_+<u_-时,u_o=-U_{OPP}$
- 虚短不存在,虚断仍存在。
放大电路的模型
是一个双端口网络
对输入端,可等效为输入电阻
对输出端,可等效为受控电压源或受控电流源

电压放大模型:
- $A_{vo}$:负载开路时的电压增益
- $R_i$:输入电阻
- $R_o$:输出电阻
- $V_o=A_{vo}v_i\frac{R_L}{R_o+R_L}$
- $A_v=\frac{v_o}{v_i}=A_{vo}\frac{R_L}{R_o+R_L}$
- 主要由负载影响增益
- 输出电阻越小越好
电流放大模型:
- $A_{is}$:负载短路时的电流增益
- $i_o=A_{is}i_i\frac{R_o}{R_o+R_L}$
- $A_i=\frac{i_o}{i_i}=A_{is}\frac{R_o}{R_o+R_L}$
- 主要由负载影响增益
- 输入电阻越小越好
主要技术指标
放大倍数:
- 电压放大倍数$\dot{A_u}=\frac{\dot{U_o}}{\dot{U_i}}$
- 源电压放大倍数$\dot{A_{us}}=\frac{\dot{U_o}}{\dot{U_s}}$
- 电流放大倍数$\dot{A_i}=\frac{\dot{I_o}}{\dot{I_i}}$
- 源电流放大倍数$\dot{A_{is}}=\frac{\dot{I_o}}{\dot{I_s}}$
- 功率放大倍数$A_{P}=\frac{P_o}{P_i}$
- 输入电阻$R_i$
- 输出电阻$R_o$:负载开路时在输出端加电压源
- 通频带BW:放大倍数不小于中频电压放大倍数$A_0$的$1/\sqrt{2}$时对应的频率范围
4-2 放大电路的分析方法
分析要求
放大电路建立正确的静态,是保证动态工作的前提
放大电路的分析主要指直流特性与交流特性的分析,须区分静态与动态,直流通路与交流通路
- 静态:$-\mu_i=0$,又称直流工作状态
-
动态:$-\mu_i\neq0$,又称交流工作状态
- 直流通路:直流量传递的途径,耦合电容开路
- 交流通路:交流量传递的途径,直流电源和耦合电容短路
静态分析
分析对象:静态工作点Q:$I_{BQ},I_{CQ},U_{CWQ}$以及$U_{GSQ},I_{DQ},U_{DSQ}$
分析路径:直流通路
分析方法:
- 计算法:画出放大电路的直流通路,以两个固定电位间的通路为着眼点,根据KVL、KCL列方程
- 图解分析法:
- 双极型:在输入特性曲线上画出静态工作点,得到$I_{BQ},U_{BEQ}$,在输出特性曲线上画出静态工作点,得到$I_{CQ},U_{CEQ}$
- 场效应管:在转移特性曲线上画出静态工作点,得到$I_{DQ},U_{GSQ}$,在输出特性曲线上画出静态工作点,得到$I_{CQ},U_{CEQ}$
动态分析
分析对象:$A_u,R_i,R_o$
分析路径:交流通路
分析方法:
- 图解分析法:
- 画出交流通路
- 列出输出回路交流方程
- 在输出特性曲线中画出负载线:过Q且斜率为$-\frac{1}{R’_L}$的直线
- 微变等效电路法:微变使得近似线性
- 画出交流通路
- 将三极管用等效模型代替
- 整理出放大电路的等效电路
- 基于KCL、KVL列方程
结论:
- 交流负载线与直流负载线交于Q
- 直流负载线反映静态时电压电流变化关系,用于确定Q
- 交流负载线反映动态时电压电流变化关系,是交流输入下Q的运动轨迹
- 交流负载电阻$R’_L:\frac{1}{R’_L}=\frac{1}{R_L}+\frac{1}{R_c}$,故交流负载线更陡
4-3 共射放大电路
共发射极组态放大电路的组成
三极管VT:放大作用
负载电阻$R_C,R_L$:将变化的电流转化为电压输出
偏置电路$V_{CC},R_B,R_C$:提供直流偏置
耦合电容$C_1,C_2$:隔直流,通交流

放大电路的构成原则:
- 与放大管种类匹配的电源极性
- 合理设置静态工作点Q
- 外加输入信号加在发射结上
- 将交流量转换成电压,输出端须接负载电阻$R_C$
静态分析
直流负载线的确定方法:
- $u_{CE}=V_{CC}-i_CR_C$
- 在输出特性曲线上确定两点$V_{CC},V_{CC}/R_C$
- $u_{BE}=V_{CC}-i_BR_b$
- 在输入特性曲线上作出输入负载线,两线交点即为Q
动态分析
交流负载线的确定方法:
- 通过输出特性曲线上的Q点作一条斜率为$-1/R’_L$直线
- 两个特殊点$(0,\frac{V_{CE}}{R’L}+I_C),(V{CE}+I_CR’_L,0)$
饱和失真:放大电路工作到三极管的饱和区引起的非线性失真
- NPN管:输出电压表现为底部失真
截止失真:放大电路工作到三极管的截止区引起的非线性失真
- NPN管:输出电压表现为顶部失真
放大电路的最大不失真输出幅度:工作点Q要设置在输出特性曲线放大区的中间部位
电压放大倍数:$\dot{A_u}=\frac{\dot{U_o}}{\dot{U_i}}=\frac{\beta{R’L}}{r{be}}$
输入电阻:$R_i=\frac{\dot{U_i}}{\dot{I_i}}=R_B//r_{be}\approx{r_{be}}$
| 输出电阻:$R_o=\frac{\dot{U_o}}{\dot{I_o}} | _{R_L=\infty,\dot{U_S}=0}=R_C$ |
源电压放大倍数:$\dot{A_{us}}=\frac{\dot{U_o}}{\dot{U_S}}=\dot{A_u}\frac{R_i}{R_i+r_S}$

4-4 放大电路的稳定偏置
Q点对电路性能的影响:$u_{BE},\beta,I_{CEO}$均为温度的函数
分压式偏置电路
须有$I_{RB1}»I_{BQ},U_B»U_{BEQ}$

直流分析:
- $U_B=V_{CC}R_{B2}/(R_{B1}+R_{B2})$
- $I_{BQ}=I_{CQ}/\beta$
- $I_{CQ}=I_{EQ}=(U_B-U_{BEQ})/R_E$
- $U_{CEQ}=V_{CC}-I_{CQ}(R_C+R_E)$
交流分析:
- 电压放大倍数:$\dot{A_u}=-\frac{\beta\cdot{R’L}}{r{be}+(1+\beta)R_E}$
- 输入电阻:$[r_{be}+(1+\beta)R_E]//R’_B$
- 输出电阻:忽略$r_{ce}$的影响:$R_o\approx{R_C}$
4-5 共基及共集电极放大电路
共基组态基本放大电路
直流分析:与共射放大电路一致
交流分析
- 电压放大倍数:$\dot{A_u}=u_o/u_i=\frac{\beta{R’L}}{r_{be}}$
- 输入电阻:$R_i=R_E//R’i\approx\frac{r{be}}{1+\beta}$
- 输出电阻:$R_o\approx{R_C}$
特点:
- 同相放大器
- 输入电阻比共射电路小
- 输出电阻与共射电路相同

共集电极放大电路
电压放大倍数:$\dot{A_u}=\frac{(1+\beta)R’L}{r{be}+(1+\beta)R’_L}\approx1$
输入电阻:$R_i=R_{B1}//R_{B2}//R’_i$
输出电阻:$R_o=R_E//\frac{r_{be}+r’_s}{1+\beta}$
特点:
- 射极输出器=电压跟随器
- 输入电阻高
- 输出电阻低

4-7 场效应管放大电路
组态:
- 共源:相当于共射极
- 共栅:相当于共基极
- 共漏:相当于共集电极
共源组态放大电路
静态分析:
- 计算法:
- $U_{GS}=U_G-U_S=-I_DR_S$
- $I_D=I_{DSS}(1-\frac{U_{GS}}{U_{GS(off)}})^2$
- $U_{DS}=V_{DD}-I_D(R_D+R_S)$
- 图解法
交流分析:
- 电压放大倍数$\dot{A_u}=-g_mR’L,R’_L=R_D//R_L,g_m=-\frac{2}{U{GS(off)}}\sqrt{I_{DQ}I_{DSS}}$
- 输入电阻$R_i=R_g$
- 输出电阻$R_o=R_d$
共漏组态放大电路
静态分析:
- $U_G=\frac{R_{G2}}{R_{G1}+R_{G2}}V_{DD}$
- $I_D=I_{DSS}(1-\frac{U_{GS}}{U_{GS(off)}})^2$
- $U_{GS}=U_G-I_DR_S$
交流分析:
- 电压放大倍数$\dot{A_u}=\frac{G_mR’_L}{1+g_mR’_L},R’_L=R_S//R_L$
- 输入电阻$R_i=R_{G3}+(R_{G1}//R_{G2})$
- 输出电阻$R_o=R_S//r_{ds}//\frac{1}{g_m}\approx{R_S}//\frac{1}{g_m}$
动态性能比较表

1 运算放大器的线性应用
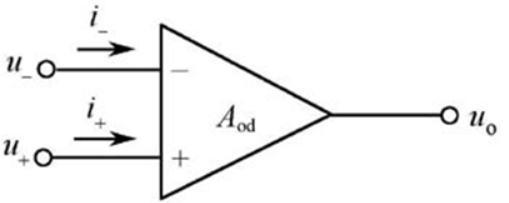
1-1 理想运放的特性
共模信号:两信号和的一半,即均值
差模信号:两信号差的一半
运放具有放大差模、抑制共模的特点
理想运放的技术指标
开环差模增益:$A_{od}=\infty$
差模输入电阻:$r_{id}=\infty$
输出电阻:$r_o=0$
共模抑制比:$K_{CMR}=\infty$
一般在原理性分析时,运算放大器都可视作理想的。
在线性区工作时:
- 虚短:==$u_o=A_{od}(u_+-u_-)$==,线性工作区域下可以把输入端看作等电位
- 虚断:输入电阻趋近无穷,$i_+=i_-=0$,线性状态下可把两输入端看作开路。
在非线性区工作时:
- $u_+>u_-时,u_o=+U_{OPP}$
- $u_+<u_-时,u_o=-U_{OPP}$
- 虚短不存在,虚断仍存在。
1-2 比例运算电路
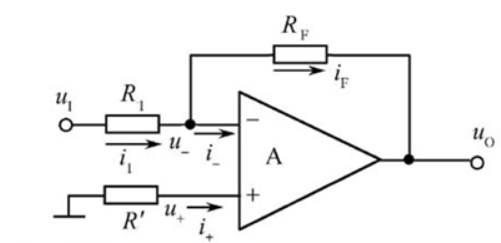
反相比例运算电路
深度负反馈
平衡电阻R’在运放足够理想时无效,在实际中有效,$\frac{1}{R’}=\frac{1}{R_1}+\frac{1}{R_F}$
$\frac{u_I-u_-}{R_1}=\frac{u_–u_o}{R_F}\Rightarrow{u_o}=-\frac{R_F}{R_1}u_I$
当$R_F=R_1$时,$u_o=-u_I$,是为倒相器
虚地:同相、反相端电位都为0
- 优点:由于共模信号为0,计算精度高;
- 缺点:反相端电阻即为$R_I$,输入电阻过小
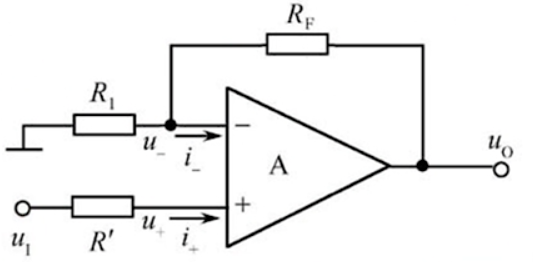
同相比例运算电路
${u_o}=(1+\frac{R_F}{R_1})u_I$
当$R_F=0,R_1=\infty$时,$u_o=u_I$,是为电压跟随器
- 优点:输入电阻无穷大(由此可完全获得信号)
- 缺点:不虚地
进行阻抗变换,起电压隔离的作用
1-3 加法和减法电路
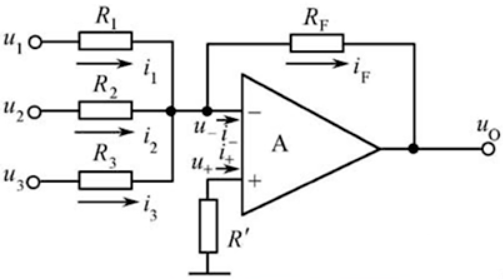
反相加法器
$u_o=-(\frac{u_1}{R_1}+\frac{u_2}{R_2}+\frac{u_3}{R_3})R_F$
优点:
- 要改变权值,只要改动对应支路
- 虚地,共模小
同相加法器
${u_o}=(1+\frac{R_F}{R_1})u_+$
$u_+=(\frac{u_1}{R’_1}+\frac{u_2}{R’_2}+\frac{u_3}{R’_3})R_P$,其中$R_P=R’_1、R’_2、R’_3、R’并联$
缺点:
- 结果复杂
- 调试不便
- 不虚地
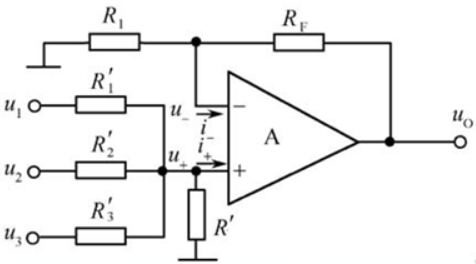
加法器实现的减法器
$u_o=\frac{R_f}{R_2}u_{i2}-\frac{R_f}{R_1}u_{i1}$
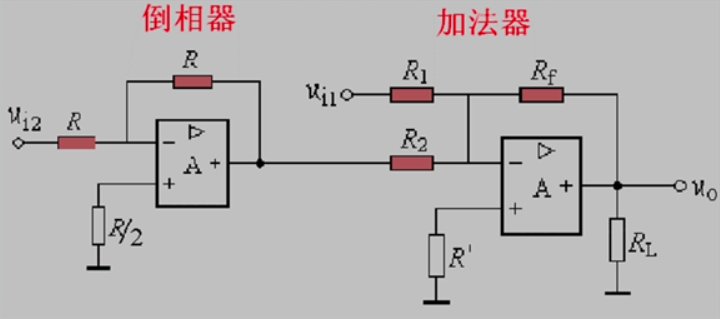
差动减法器
$u_{o1}=-\frac{R_f}{R_1}u_{i1}$
$u_{o2}=(1+\frac{R_f}{R_1})\frac{R’}{R’+R_2}u_{i2}$
当$\frac{R_f}{R_1}=\frac{R’}{R_2}$时,$u_o=\frac{R_f}{R_1}(u_{i2}-u_{i1})$
缺点:
- 不虚地
- 共模大
- 要选共模抑制比大的运放
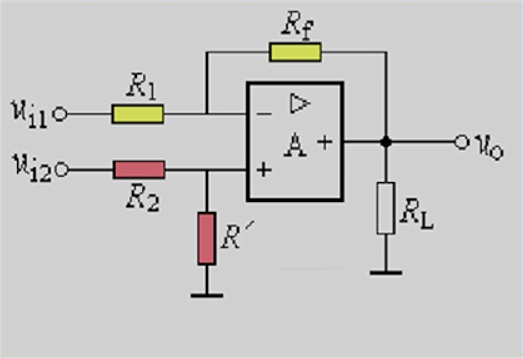
1-4 积分、微分、指数、对数电路
积分运算电路
$u_o=-\frac{1}{RC}\int{u_i}dt$
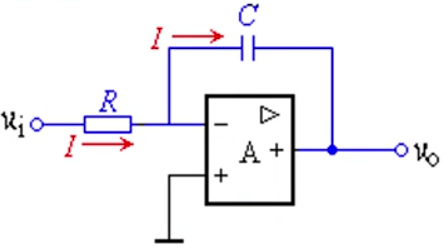
微分运算电路
$u_o=-RC\frac{du_I}{dt}$
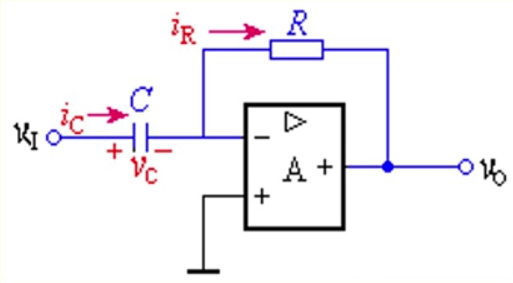
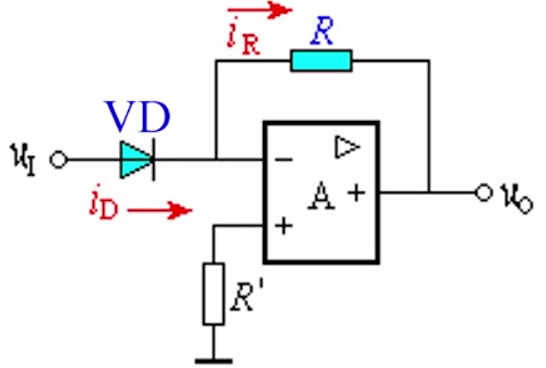
对数运算电路
$u_o=U_Tln\frac{u_I}{RI_S}$,其中$i_D\approx{I_S}e^\frac{U_D}{U_T}$
通常用三极管解成二极管,以增大工作区域
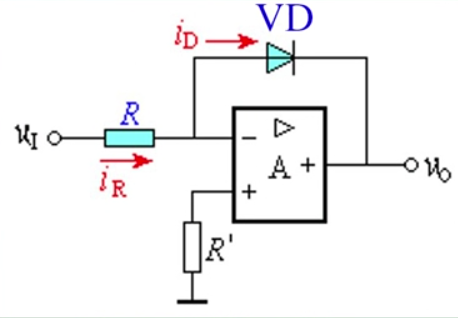
指数运算电路
$u_o=-RI_Se^\frac{U_D}{U_T}$
1-5 运放运算电路的应用
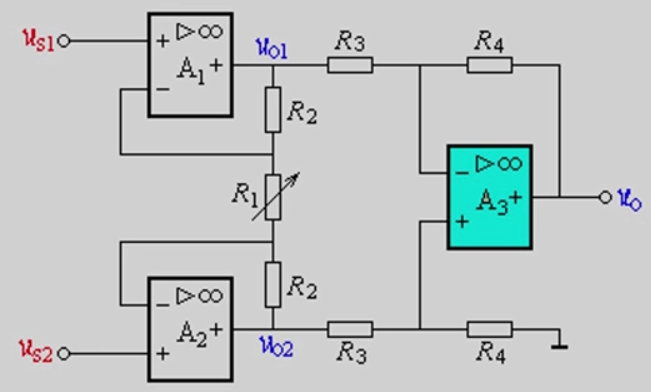
数据放大器
特点:
- 高共模抑制比
- 高输入阻抗
- 高放大倍数
$u_o=\frac{R_4}{R_3}(1+\frac{2R_2}{R_1})(u_{S2}-u_{S1})$
$R_1$作用:调节增益
电流-电压变换器
$u_o=-i_SR_f$
负载电阻不变时可视为电流放大电路
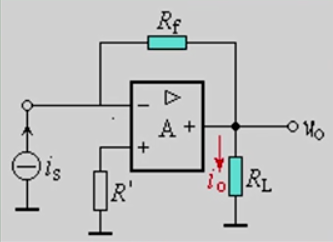
电压-电流变换器
- 负载不接地 $i_o=\frac{u_S}{R}$
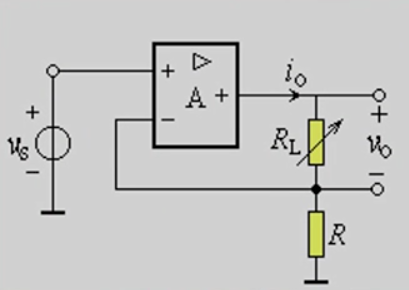
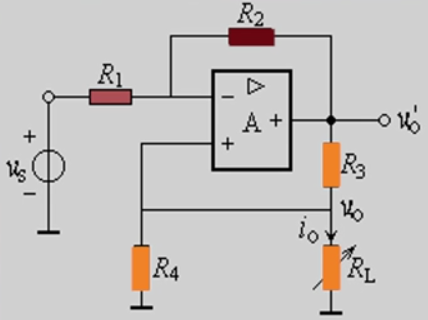
- 负载接地 $i_o=-\frac{R_2}{R_1}\times\frac{u_S}{R_3+(\frac{R_3}{R_4}-\frac{R_2}{R_1})R_L}$,其中须避免分母为0。
1-6 一阶有源滤波器
有源滤波器可以放大信号,负载要求低
滤波器的技术指标:
- 通带增益$A_{uf}$
- 通带截止频率$f_0$
$A_{uf}=1+\frac{R_F}{R_1}$
传递函数:$A(s)=\frac{A_{uf}}{1+\frac{s}{\omega_0}}$,其中$\omega_0=\frac{1}{RC}$
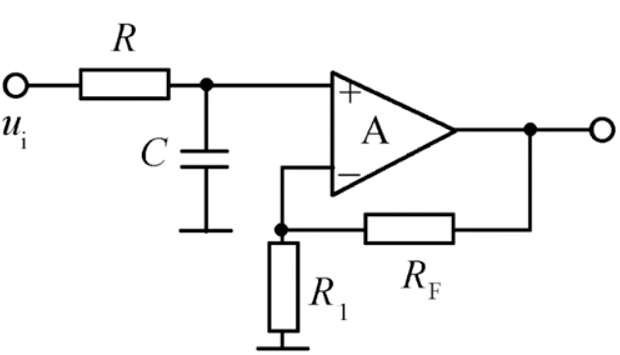
一阶低通
1-7 二阶有源滤波器
二阶低通有源滤波器
$A_{uf}=1+\frac{R_F}{R_1}$
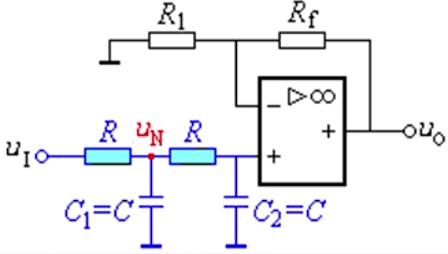
二阶压控型低通有源滤波器
传递函数:$A_u(s)=\frac{A_{uf}}{1+(3-A_{uf})sCR+(sCR)^2}$
频率响应:$\dot{A_u}\frac{A_{uf}}{1-(\frac{f}{f_0})^2+j(3-A_{uf})\frac{f}{f_0}}$
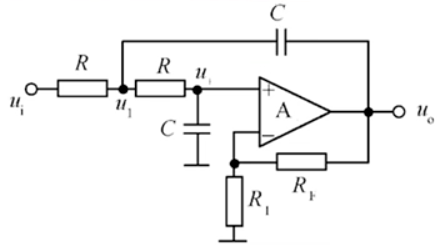
二阶压控型高通有源滤波器
$A_{uf}=1+\frac{R_F}{R_1}$
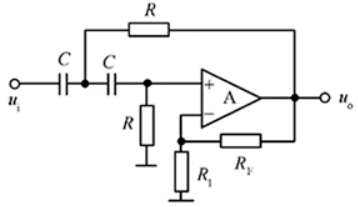
二阶带通有源滤波器
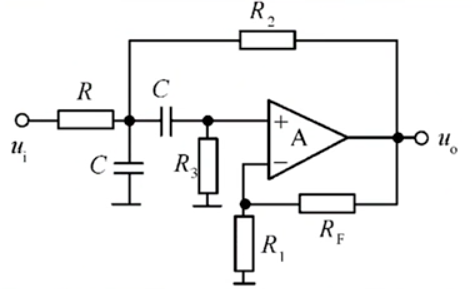
二阶带阻有源滤波器
并联一阶低通和一阶高通
2 运算放大器的非线性运用
2-1 电压比较器
参考电压$V_T$:使输出电压跳变时的输入电压,又称阈值/门限电压,输入电压小于参考电压时输出正的最大电压,反之则输出负的最大电压
特性:非线性开关特性
普通的开环运放就能构成比较器:e.g.将一个输入端接地,即形成简单的过零电压比较器
对于开环或正反馈运放:
- +端电位高,正饱和
- -端电位高,负饱和
基本比较器电路

$VD_Z$:稳压管,用于限幅

- 输出电压在$[-U_Z,U_Z]$之外时,稳压管被击穿,运放在线性区域工作
- 输出电压在$[-U_Z,U_Z]$之内时,稳压管不被击穿,运放在开环区域工作
2-2 集成电压比较器和窗口比较器
集成电压比较器往往能和运放互换:
- 运放作比较器时响应较慢
- 比较器作运放时由于不强调线性,信号较大时易失真
集成电压比较器LM311


窗口比较器
输入电压在$(U_L,U_H)$内时输出低电平,其它情况输出高电平
$U_L=\frac{R_2}{R_1+R_2}(V_{CC}-2U_D)$
两半导体用于隔离,以免输出电流过大或输出状态不确定

2-3 555定时器
由窗口比较器、RS触发器和三极管组成
| > | 输入 | > | 输出 | |
|---|---|---|---|---|
| $\bar{R}$ | TH | $\overline{TR}$ | VT | Q |
| 0 | X | X | 导通 | 0 |
| 1 | $<\frac{2}{3}V_{CC}$ | $<\frac{1}{3}V_{CC}$ | 截止 | 1 |
| 1 | $>\frac{2}{3}V_{CC}$ | $>\frac{1}{3}V_{CC}$ | 导通 | 0 |
| 1 | $<\frac{2}{3}V_{CC}$ | $>\frac{1}{3}V_{CC}$ | 不变 | 不变 |

2-4 施密特触发器
特点:阈值电压有两个,即有回差
用比较器构成
$u_o=U_Z$时:
- 上限阈值:$U_{T_+}=\frac{R_1}{R_1+R_2}U_Z$
- 下限阈值:$U_{T_-}=-\frac{R_1}{R_1+R_2}U_Z$

反相输入

同相输入

2-5 单稳态触发器
应用:控制、延时、整形

2-6 矩形波振荡电路
用电压比较器构成:
- 构成要点:
- 比较器能实现翻转
- 周期控制(RC控制电路)
- 工作原理:
- 非稳态电路
- 参数:
- 周期:$T=2R_TC_Tln(1+\frac{2R_1}{R_2})$
- 占空比:50%

占空比可调的矩形波振荡电路

单电源矩形波振荡电路
$\begin{cases}u_o=V_{CC}时,U_+=\frac{2}{3}V_{CC}\u_o=0时,U_-=\frac{1}{3}V_{CC}\end{cases}$

555构成的振荡电路
占空比不是50%
$t_1=\frac{2}{3}(R_1+R_2)C,t_2=\frac{2}{3}R_2C,T=t_1+t_2$

2-7 三角波振荡电路
由比较器和积分器组成
参数分析:
- 幅度:$2U_Z\frac{R_1}{R_2}$
- 周期:$\frac{4R_1R_4C}{R_2}$
